RATTERN - The Room Pattern
It was decided to make a parquet floor in a room of size NxM. The idea is to lay out some pattern on the floor. The parquet tiles with which the floor of the room looks best consist of squares 1x1, each of which can be either white or black. The required color of each square of the room is specified on the map of the room.
There are four different forms of parquet tiles:
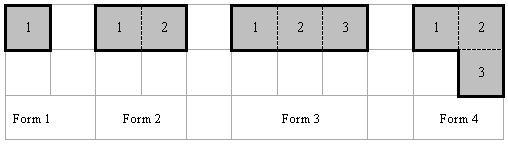
Squares of one parquet tile can be painted differently. Some types of tiles can be of identical shape, but painted differently. Tiles of different types can have different cost. The number of available tiles of each type is not limited. Tiles are allowed to be turned around somehow (by an angle which is a multiple of 90 degrees), but it is not permitted to break a tile or to put it face sheet downwards. Initially, any part of the floor can be already laid out by tiles. You are requested to calculate the minimal cost of the tiles necessary to pave the remaining part of the room.
Input
t – the number of test cases, then t test cases follow.
In the first line of each test case three numbers are written: N, M (the sizes of the room) and K (number of accessible types of tiles). [1<= N, M <= 8], [1 <= K <= 10].
Next there is a description of the desired painting of the floor. The description is given in the form of N lines of M numbers each, where 0 denotes the color white, 1 - the color black, 2 - a square which has already been covered by a tile. In the last K lines the descriptions of available types of tiles are given in the following format:
[Form] [cost] [painting] where:
[Form] is a number from 1 to 4, describing the form of a tile (see figure above)
[Cost] is an integer not larger than 10000, describing the cost of one tile of the type.
[Painting] is a sequence of between one and three numbers 0 or 1. Its length is the same as the number of squares of which the tile consists, and the respective numbers describe colors of square tiles in the order in which the squares are numbered in the figure.
Output
For each test case output one integer: the minimal cost of laying the remaining part of the parquet, or -1 if the task cannot be performed.
Example
Input:
1 4 3 3 2 2 2 2 0 0 2 1 2 2 2 2 2 10 0 0 1 5 1 4 6 0 0 1
Output:
15
hide comments
|
|
:D:
2010-09-07 20:18:21
I don't think so, but you may have to use proper data packing, algorithm and container. |
|
|
刘启鹏:
2010-07-01 12:44:12
time limit is toooooooo strict |
| Added by: | Roman Sol |
| Date: | 2005-03-05 |
| Time limit: | 17s |
| Source limit: | 20000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | The Moscow Olympiad on computer science 2004/05. Correspondence round. |

 RSS
RSS