RECTNG1 - Rectangles
There are n rectangles drawn on the plane. Each rectangle has sides parallel to the coordinate axes and integer coordinates of vertices.
We define a block as follows:
- each rectangle is a block,
- if two distinct blocks have a common segment then they form the new block otherwise we say that these blocks are separate.
Examples
The rectangles in Figure 1 form two separate blocks.
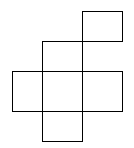
The rectangles in Figure 2 form a single block
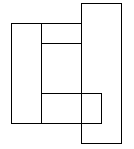
Task
Write a program that for each test case:
- reads the number of rectangles and coordinates of their vertices;
- finds the number of separate blocks formed by the rectangles;
- writes the result to the standard output.
Input
The number of test cases t is in the first line of input, then t test cases follow separated by an empty line.
In the first line of a test case there is an integer n, 1 ≤ n ≤ 7000, which is the number of rectangles. In the following n lines there are coordinates of rectangles. Each rectangle is described by four numbers: coordinates x, y of the bottom-left vertex and coordinates x, y of the top-right vertex. All these coordinates are non-negative integers not greater than 10000.
Output
For each test case you should output one line with the number of separate blocks formed by the given rectangles.
Example
Sample input: 1 9 0 3 2 6 4 5 5 7 4 2 6 4 2 0 3 2 5 3 6 4 3 2 5 3 1 4 4 7 0 0 1 4 0 0 4 1 Sample output: 2
hide comments
|
|
:D:
2012-05-03 10:47:03
O(N^2) can pass. |
|
|
Szabolcs Szucs:
2010-04-09 22:35:49
what is the answer for these rectangles?:
|
|
|
Luke Pebody:
2010-01-07 14:03:03
The answer seems to be 3? It seems that the pairs of rectangles that share segments are:
|
| Added by: | Michał Czuczman |
| Date: | 2004-08-10 |
| Time limit: | 1.279s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | 5th Polish Olympiad in Informatics, stage 3 (Wojciech Rytter) |

 RSS
RSS