SAMER08K - Shrinking Polygons
A polygon is said to be inscribed in a circle when all its vertices lie on that circle. In this problem you will be given a polygon inscribed in a circle, and you must determine the minimum number of vertices that should be removed to transform the given polygon into a regular polygon, i.e., a polygon that is equiangular (all angles are congruent) and equilateral (all edges have the same length).
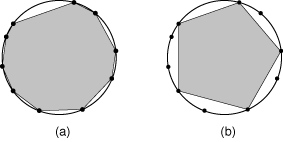
When you remove a vertex v from a polygon you first remove the vertex and the edges connecting it to its adjacent vertices w1 and w2, and then create a new edge connecting w1 and w2. Figure (a) below illustrates a polygon inscribed in a circle, with ten vertices, and figure (b) shows a pentagon (regular polygon with five edges) formed by removing five vertices from the polygon in (a).
In this problem, we consider that any polygon must have at least three edges.
Input
The input contains several test cases. The first line of a test case contains one integer N indicating the number of vertices of the inscribed polygon (3 ≤ N ≤ 104). The second line contains N integers Xi separated by single spaces (1 ≤ Xi ≤ 103, for 0 ≤ i ≤ N -1). Each Xi represents the length of the arc defined in the inscribing circle, clockwise, by vertex i and vertex (i+1) mod N. Remember that an arc is a segment of the circumference of a circle; do not mistake it for a chord, which is a line segment whose endpoints both lie on a circle.
The end of input is indicated by a line containing only one zero.
Output
For each test case in the input, your program must print a single line, containing the minimum number of vertices that must be removed from the given polygon to form a regular polygon. If it is not possible to form a regular polygon, the line must contain only the value -1.
Example
Input: 3 1000 1000 1000 6 1 2 3 1 2 3 3 1 1 2 10 10 40 20 30 30 10 10 50 24 26 0 Output: 0 2 -1 5
| Added by: | Diego Satoba |
| Date: | 2008-11-23 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | C CSHARP C++ 4.3.2 CPP JAVA PAS-GPC PAS-FPC |
| Resource: | South American Regional Contests 2008 |

 RSS
RSS