SCPC11F - GO
In the game of Go, two players alternate placing black and white stones on lattice points of an n × n grid, each attempting to surround as much territory (i.e., regions of unfilled lattice points) as possible. At the end of the game, the score for each player is the total area of the territory surrounded by his or her stones. Given the locations of black and white stones on a Go board at the end of a match, your task is to compute the score of each player in order to determine the winner.
Formally, two grid lattice points with coordinates (r, c) and (r', c') are adjacent if |r − r'| + |c − c'| = 1.
A connected region of unfilled lattice points belongs to one player’s territory if all adjacent filled lattice points contain stones belonging to that player (see Figure 1). Finally, a player’s score consists of the number of unfilled lattice points in his or her territory.
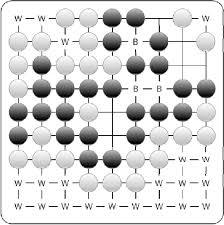
Note that the scoring of Go boards described here does not correspond exactly to the real game of Go: we make the simplifying assumptions that all “disputes” have been settled so that any territories surrounded by stones of both colors are considered neutral, and that all groups on the board are considered “alive.”
Figure 1: Diagram of a 9 × 9 Go board. Unfilled lattice points belonging to black’s territory are marked with B, and unfilled lattice points belonging to white’s territory are marked with W. Neutral unfilled lattice points are unmarked. In the game above, white wins by 21 − 3 = 18.
Input
The input test file will contain multiple cases, each consisting of three lines. Each test case begins with a line containing three integers, n (where 1 ≤ n ≤ 19), b, and w (where b ≥ 0,w ≥ 0 and 1 ≤ b + w ≤ n2). Here, n denotes the size of the board, b is the number of black pieces placed, and w is the number of white pieces placed. The second line of each test case contains b pairs of integers r1 c1 ... rb cb (where 1 ≤ ri , ci ≤ n) indicating the positions of the b black stones. The third line of each test case contains w pairs of integers r'1 c'1 ... r'w c'w (where 1 ≤ r'i , c'i ≤ n) indicating the positions of the w white stones. No two stones will be located at the same lattice point. Input is terminated by a single line containing only the number 0; do not process this line.
Output
For each test case, print either “White wins by ”, “Black wins by ”, or “Draw”.
Example
Input: 1 1 0 1 1 2 0 1 1 1 5 12 4 1 1 1 2 1 3 2 1 2 3 3 1 3 3 4 1 4 3 5 1 5 2 5 3 1 4 2 4 3 4 3 5 0 Output: Draw White wins by 3 Black wins by 1
| Added by: | Ali Arous |
| Date: | 2011-10-19 |
| Time limit: | 2s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | Syrian Collegiate Programming Contest 2011 |

 RSS
RSS