TAP2012A - Awari 2
[The original version of this problem (in Spanish) can be found at http://www.dc.uba.ar/events/icpc/download/problems/taip2012-problems.pdf]
Awari is a one-player game from the Antilles, which is played with boxes and stones instead of cards. A particular variant of Awari is played with N boxes numbered from 1 to N, each containing at the beginning of the game zero or more stones. The rules of this game are very simple, because there is only one type of valid move, consisting of choosing a box numbered i containing exactly i stones, and then taking those stones from the box in order to use them to add a single stone to every box numbered 1 through i-1; the remaining stone is then kept by the player. These moves are applied in succession as long as there exists a box i containing exactly i stones. When this is no longer true, the game ends. The player wins if at this stage every box is empty, and looses otherwise.
In the following figure, on the left hand side there is a possible initial state of a game with N = 5 boxes (the circles) containing P1 = 0, P2 = 1, P3 = 3, P4 = 0 and P5 = 2 stones (the black dots). If box number 3, containing P3 = 3 stones, was chosen to make the next move, then the resulting configuration would be the one shown on the right hand side of the figure. Additionally, the player would now have one stone in his power.
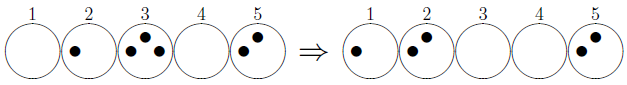
Given the initial state of the boxes, you should determine if it is possible to win the game, that is, if there is a sequence of valid moves after which all the boxes are left empty.
Input
Each test case is described using two lines. The first line contains an integer N, indicating the number of boxes (1 ≤ N ≤ 500). The second line contains N integer numbers Pi, representing the number of stones in the boxes at the beginning of the game, from box 1 to box N in that order (0 ≤ P_i ≤ 500 for i = 1, ..., N). In every test case there is at least one non-empty box, that is there exists i from 1 to N such that Pi ≠ 0. The end of the input is signalled by a line containing the number -1.
Output
For each test case, you should print a single line containing a single character. This character should be the uppercase letter 'S' if it is possible to win the game; otherwise, it should be the uppercase letter 'N'.
Example
Input: 5 0 1 3 0 2 4 1 1 3 0 3 1 2 3 -1 Output: N S N
hide comments
|
|
nadstratosfer:
2017-11-22 15:15:44
Decided to write the game in Python for fun, made a couple observations that turned it into a simulation. Then wasted 2 hours looking for O(n) to no avail. WTF! Frustrating but at least the simulation gets AC ;) |
|
|
Vijay Jain:
2013-06-29 05:54:18
nice prob :) |
|
|
:D:
2012-10-05 16:29:38
First you empty the first box and have (0,1,3) (it's a valid move, read the description again). Then (0,1,3) => (1,2,0) => (0,2,0) => (1,0,0) => (0,0,0). |
|
|
Vaishali Behl:
2012-10-05 16:29:38
Can someone explain how a win is possible in the second test case? How can one empty the first box? |
| Added by: | Fidel Schaposnik |
| Date: | 2012-10-04 |
| Time limit: | 2s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | Argentinian Programming Tournament 2012 |

 RSS
RSS