TREE - Another Counting Problem
Tree is an important data structure in Computer Science. Of all trees we work with, Binary Tree is probably the most popular one. A Binary Tree is called a Strictly Binary Tree if every nonleaf node in a binary tree has nonempty left and right subtrees. Let us define a Strictly Binary Tree of depth d, as a Strictly Binary Tree that has at least one root to leaf path of length d, and no root to leaf path in that tree is longer than d. So let us use a similar reasoning to define a generalized structure.
An n-ary Tree is called a Strictly n-ary Tree if every nonleaf node in an n-ary tree has n children each. A Strictly n-ary Tree of depth d can now be defined as a Strictly n-ary Tree that has at least one root to leaf path of length d, and no root to leaf path in that tree is longer than d.
Given the value of n and depth d, your task is to find the number of different strictly n-ary trees of depth d.
The figure below shows the 3 different strictly binary trees of depth 2.
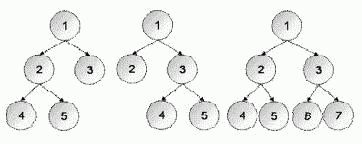
Input
Input consists of several test cases. Each test case consists of two integers n (0 < n <= 32), d (0 <= d <= 16). Input is terminated a test case where n=0 and d=0, you must not process this test case.
Output
For each test case, print three integers, n, d and the number of different strictly n-ary trees of level d, in a single line. There will be a single space in between two integers of a line. You can assume that you would not be asked about cases where you had to consider trees that may have more than 210 nodes in a level of the tree. You may also find it useful to know that the answer for each test case will always fit in a 200 digit integer.
Example
Input: 2 0 2 1 2 2 2 3 3 5 0 0 Output: 2 0 1 2 1 1 2 2 3 2 3 21 3 5 58871587162270592645034001
hide comments
|
|
navin_jr07:
2015-10-13 07:50:01
using the additional library for storing the output.. Its worked for me.. Last edit: 2017-02-17 17:21:22 |
|
|
Deepak Gupta:
2014-12-14 16:57:54
Considering max number of nodes on a level to be 999999 worked for me. |
|
|
:D:
2011-06-11 18:29:32
There ARE trees with levels bigger that 2^10. The general input constraints seem to hold. You can still assume that number of digits is at most 200 (info taken from the forum). |
| Added by: | Nguyen Van Quang Huy |
| Date: | 2006-02-14 |
| Time limit: | 0.5s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO |
| Resource: | acm.uva.es |

 RSS
RSS