TREE1 - Tree
Consider an n-vertex binary search tree T containing n keys 1, 2 ... n. A permutation p = [p1 ... pn] of the integers 1, 2 ... n is said to be consistent with the tree T if the tree can be built from the empty one as the result of inserting integers p1, p2 ... pn. Find how many permutations are consistent with the tree T.
Illustration
Exactly 2 permutations are consistent with the tree in the figure below.
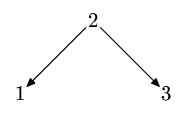
Task
Write a program that for each data set from a sequence of several data sets:
- reads from the input file a description of an input tree T,
- computes the number of permutations consistent with T,
- writes the result to output.
Input
The first line of the input file contains one positive integer d not larger than 10. This is the number of data sets. The data sets follow. Each set of data occupies two consecutive lines of the input file. The first line contains only one integer n, 1 <= n <= 30. This is the number of vertices of the tree. The second line contains a sequence of n integers separated by single spaces. The integers are keys in the input tree given in the prefix order. The first integer in the sequence is the key from the root of the tree. It is followed by the keys from the left subtree written in the prefix order. The sequence ends with the keys from the right subtree, also given in the prefix order.
Output
For each i = 1 ... d, your program should write to the i-th line of output the number of permutations consistent with the tree described in the i-th data set.
Example
Sample input: 5 3 2 1 3 3 1 2 3 1 1 4 2 1 3 4 4 1 4 2 3 Sample output: 2 1 1 3 1
hide comments
|
|
iostream:
2012-12-28 08:13:53
what to do for equal numbers?? |
|
|
!n[10]se:
2011-02-23 00:40:27
Yes the answer exceeds LL. |
|
|
:D:
2011-01-27 07:21:38
No, the description says only permutations of <1;N> are given. |
|
|
tarun goyal:
2011-01-27 07:04:16
can 2 numbers be equal??? |
|
|
Kedar Joglekar:
2010-11-11 06:58:41
Does answer exceed the unsigned long long int range? |
|
|
pulkit agarwal:
2010-03-15 23:05:52
unsigned even doesn't fit I suppose |
|
|
Cihad OGE:
2009-11-12 10:11:33
is answer exceed long long int ?? |
| Added by: | adrian |
| Date: | 2004-06-08 |
| Time limit: | 5s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: NODEJS PERL6 VB.NET |
| Resource: | III Polish Collegiate Team Programming Contest (AMPPZ), 1998 |

 RSS
RSS