VZLA2019D - Drawing Polygrams
Drawing stars on the last page of a notebook is a very entertaining hobby. Did you know these cute "stars" are actually called polygrams?
Given a regular polygon with p vertices, we define a polygram p/q, as the resultant polygon obtained after connecting every i-th vertex with the (i+q)-th vertex.
You may know the polygram 5/2 as pentagram
Another example is the hexagram 6/2. Given that 6 and 2 are not coprime, this polygram is composed by two 3/1 polygrams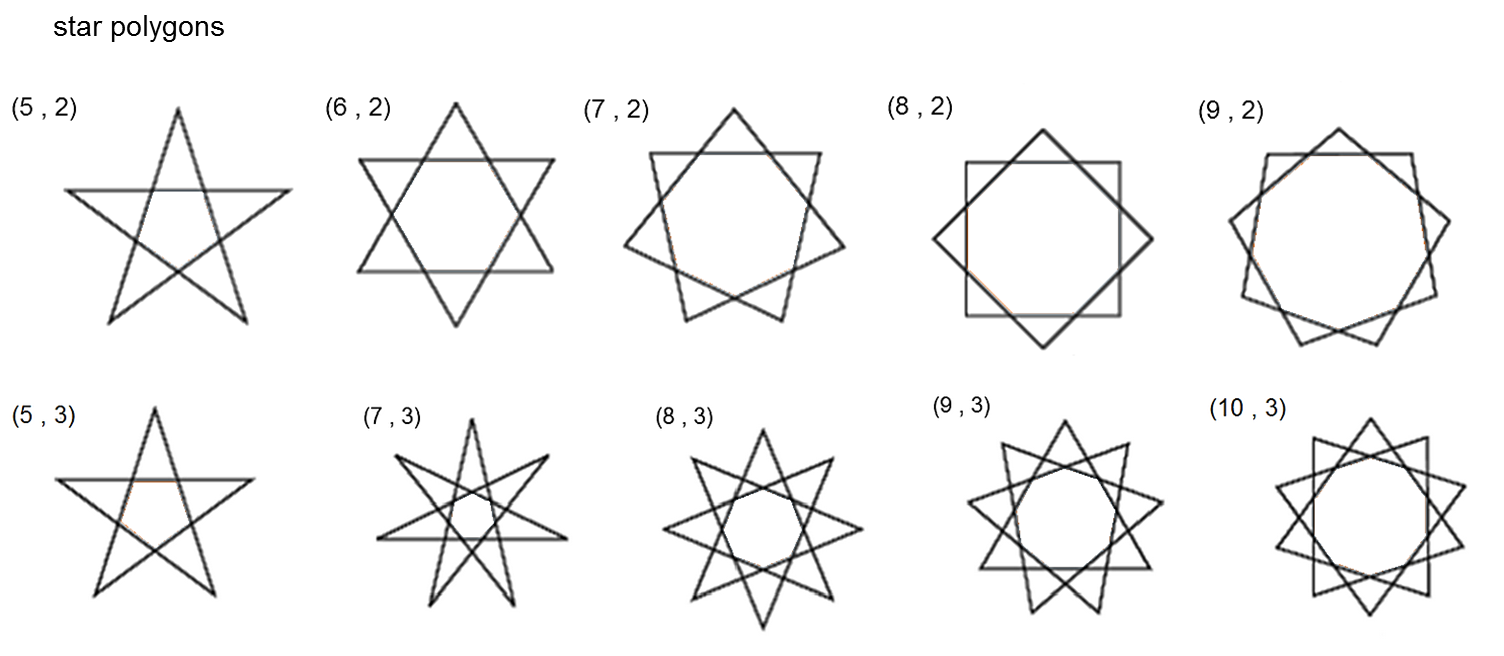
Given a regular polygon with p vertices, its radius R (the distance from its center to any vertex) and a number q, can you calculate the area of the polygram p/q?
It is guaranteed that the resultant polygon will not be degenerated, i.e q ≠ p/2 and q ≠ p
Input
The first and only line of the input contains three integers p, q and r
Output
Print in a single line the area of the resultant polygram p/q with radius r. Print the answer with exactly five decimal places
Example
Input: 5 4 2 Output: 9.51057
Input: 10 4 5
Output: 40.61496
Constraints
3 ≤ p ≤ 103
1 ≤ q < p
1 ≤ r ≤ 100
q ≠ p/2 and q ≠ p
hide comments
|
|
David:
2022-05-10 19:36:29
Thanks for fixing the image!
|
| Added by: | Samuel Nacache |
| Date: | 2019-10-27 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | Samuel Nacache - Used for Venezuelan 2019 ICPC Local Contest |

 RSS
RSS