WM06 - Soccer Choreography
Mr. Bitmann, the coach of the national soccer team of Bitland, is a perfectionist. He taught his players optimal tactics and improved their endurance and shape. So they qualified for the soccer woldcup this year. Due to his perfectionism the coach attaches importance not only to the performance in the game but also before the game. So he told the team captain in what formation the team should assemble before the national anthem is played. Since each of the 11 team members has a unique number between 1 and 11 on his shirt, he can represent the formation as a permutation of numbers.
Before the first game the coach told the captain that the team should line up in increasing order (picture (d)). But some players forgot the ordering and the orientation of the formation like in picture (a). Only player 1 has the right orientation. The coach went nearly mad when he saw this desaster! How could he solve the problem?
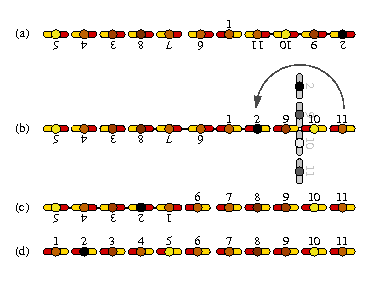
"Hmmm... I'll let my players dance!". A great idea! He took his notebook and started to create a choreography which leads to his expected formation. Due to the fact that no one of the players took dancing lessons he restricts his dance to one basic move: One player or more players who stand side by side can turn 180 degrees around the center of the move. Picture (b) contains an example: The players
-11 -10 -9 -2
(we mark players which stand in the wrong direction with a minus) can do one move to
2 9 10 11
As perfect as he is he calculated a dance with a minimum number of moves. It works perfectly and now he's planning to do dancing performances with teams with more than 11 members. So he needs your help to find optimal dancing moves...
Input
Each testcase starts with the number of team members n (0<=n< 2200). The next lines represent the formation at the beginning and the expected formation at the end of the choreography.
Output
For each testcase output m, the minimal number of moves which are necessary to reach the expected formation. The next m+1 lines should represent one possible scenario of moves.
Example
Input: 11 -5 -4 -3 -8 -7 -6 1 -11 -10 -9 -2 1 2 3 4 5 6 7 8 9 10 11 11 1 2 3 -4 -5 -6 -7 -8 -9 10 11 11 9 8 7 6 5 4 3 2 10 1 0 Output: 3 Steps -5 -4 -3 -8 -7 -6 +1 -11 -10 -9 -2 -5 -4 -3 -8 -7 -6 +1 +2 +9 +10 +11 -5 -4 -3 -2 -1 +6 +7 +8 +9 +10 +11 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11 5 Steps +1 +2 +3 -4 -5 -6 -7 -8 -9 +10 +11 +1 +2 -3 -4 -5 -6 -7 -8 -9 +10 +11 +1 -2 -3 -4 -5 -6 -7 -8 -9 +10 +11 +1 -2 -3 -4 -5 -6 -7 -8 -9 -11 -10 +11 +9 +8 +7 +6 +5 +4 +3 +2 -1 -10 +11 +9 +8 +7 +6 +5 +4 +3 +2 +10 +1
hide comments
|
|
Encho:
2014-11-19 17:20:25
Is it even possible to solve the problem currently? TL=0s seems like something just went wrong in calculating it. I highly doubt any solution can pass in under a second.
|
|
|
Francky:
2014-11-16 17:30:00
It seems all problems will be switched to cube, according to admins...
|
|
|
Min_25:
2014-11-16 09:28:13
The admin should clarify the algorithm of calculating the time limit.
|
|
|
Mitch Schwartz:
2014-05-17 01:44:11
@Encho: Congrats! My impression was also that the problem is hard but doable, and that it could (maybe) be considered medium difficulty by some solvers who are better at this type of problem than I am. Besides difficulty, I think interest in a problem is somewhat biased toward problems that are new and problems that have recently been solved or attempted by other people -- maybe it's human nature. Last edit: 2014-05-19 23:26:00 |
|
|
Encho:
2014-05-16 23:56:51
Very good problem with interesting (though difficult) theory behind it. I'm surprised there aren't many accepted solutions as the papers describing the solution are published online.
|
|
|
Mitch Schwartz:
2014-05-09 02:27:47
@Vlad Duta: Judging doesn't halt on first failure. I would assume n=0 indicates the end of test data, like many other problems. I don't see anything ambiguous about 0 or 1 steps. Each case will be a signed permutation on [1..n]; it is stated implicitly but is pretty clear in my view. (The description for n=11 is explicit, and then we are told that n could be an integer different from 11.) |
|
|
Vlad Duta:
2014-05-09 01:59:29
Is there a bug in this problem's judge? It looks like I'm passing the first two tests no matter what I'm printing... Also the input/output specifications are pretty vague. Is the input zero-terminated? What should we print if the number of steps is 0 or 1? Can we assume that every input is a signed permutation of numbers between 1 and n? |
|
|
Anmol Pandey:
2014-04-22 17:38:43
@Siddhartha Sinha
|
|
|
Mitch Schwartz:
2014-03-18 05:44:50
@ওয়াসী (Wasi): I don't know if you did it on purpose, but "tiring" and "tiresome" mean different things (demanding vs. boring, approximately). The variant is standard in the literature, and anyone who enjoys working on this problem would probably also enjoy that one. :) But for me it isn't high priority, there are other things to work on first. |
|
|
ওয়াসী (Wasi):
2014-03-12 16:38:08
@Mitch Schwartz A harder variant? Sounds cool! I hope it is not going to be that |
| Added by: | Simon |
| Date: | 2006-05-11 |
| Time limit: | 8s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | ADA95 ASM32 BASH BF C CSHARP CPP C99 CLPS LISP sbcl LISP clisp D FORTRAN HASK ICON ICK JAVA LUA NEM NICE OCAML PAS-GPC PAS-FPC PERL PHP PIKE PRLG-swi PYTHON RUBY SCM guile SCM qobi ST WHITESPACE |

 RSS
RSS