| Submit | All submissions | Best solutions | Back to list |
PROG0197 - Game of Life |
The Game of Life, is a game devised by the British mathematician John Horton Conway in 1970. The game made its first public appearance in the October 1970 issue of Scientific American, in Martin Gardner's "Mathematical Games" column. This type of game is an example of a cellular automaton, and differs from other games like Monopoly, Risk or chess, in the sense that there are no players and that one cannot win or lose.
The game board consists of a rectangular grid, and can thus be represented by a list of lists in a computer program. After a number of cells of the grid are colored, the game begins. Game of Life goes through several "generations". In order to determine whether a cell is colored in the next generation or not, a number of rules are applied on the basis of the status (alive or dead) of the neighbours. Each cell in the grid has up to 8 neighbours, except the cells at the edge of the grid that have less than 8 neighbours. Conway has experimented with a lot with different sets of rules to find a good balance. With the wrong rules more squares (in Game of Life called "cells")would be coloured ('born') than white ("dead ") so the whole board ('grid') would be coloured. Or vice versa: there are so many fields death that the whole area goes white. The rules most commonly used are the following:
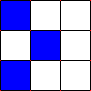
- Any live cell with two or three live
neighbours lives on to the next generation, like the middle cell in the
image below. In this example, the center cell remains coloured, because
the cell is surrounded by two other coloured cells.
- Any live cell with more than three live
neighbours dies, as if by overcrowding (that means the cel goes white).
Any live cell with fewer than two live neighbours diesas well, as if
caused by under-population. This is illustrated in the figure below. In
this example, the center cell dies, because the cell is surrounded by
more than 3 or less than 2 coloured cells.
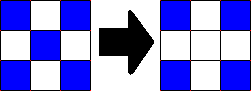
- Any dead cell with exactly three live
neighbours becomes a live cell, as if by reproduction, as shown in the
figure below. In this example, the center cell is coloured, because the
cell is surrounded by exactly 3 coloured cells.
All of these transformations are carried out simultaneously for all the cells. The art of the game is to imagine patterns that exhibit particular behaviour. There are stable patterns (simplest example: a block of four). There are patterns that go back and forth between two or more states. There are patterns that eventually disappear or change into a stable pattern. Interesting the patterns are those that move, such as the glider and the glider gun.
Assignment
- Write a function showGeneration that prints the state of a given generation. This function has one required argument: a list of lists that represents a rectangular grid. The nested lists each have the same length and only contain Boolean values. A generation is thus represented by a list of rows, and each row itself is represented through a list. At position $n$ there is True if the cell in column $n$ in that row is alive. Otherwise there is False. The living cells are represented by the letter X when printing, and the dead cells are represented by the letter O (not the number zero !!).
- Write a function numberOfNeighbours that returns the number of live neighbours of a cell for a given generation and a given cell. This function has three mandatory arguments: the first argument is the given generation, the second argument the row and the third argument the column of the cell of which the neighbours are sought.
- Use the numberOfNeighbours function to write nextGeneration, a function that returns the next generation of a given generation. This new generation is presented in the same way as the given generation, namely, as a list of lists. The given generation is passed as an argument to the function, and is not changed by the function.
Example
>>> generation = [[True] + [False] * 7 for _ in range(6)] >>> showGeneration(generation) X O O O O O O O X O O O O O O O X O O O O O O O X O O O O O O O X O O O O O O O X O O O O O O O >>> numberOfNeighbours(generation, 0, 0) 1 >>> numberOfNeighbours(generation, 1, 1) 3 >>> numberOfNeighbours(generation, 2, 2) 0 >>> next = nextGeneration(generation) >>> showGeneration(next) O O O O O O O O X X O O O O O O X X O O O O O O X X O O O O O O X X O O O O O O O O O O O O O O >>> next = nextGeneration(next) >>> showGeneration(next) O O O O O O O O X X O O O O O O O O X O O O O O O O X O O O O O X X O O O O O O O O O O O O O O >>> next = nextGeneration(next) >>> showGeneration(next) O O O O O O O O O X O O O O O O O O X O O O O O O O X O O O O O O X O O O O O O O O O O O O O O >>> next = nextGeneration(next) >>> showGeneration(next) O O O O O O O O O O O O O O O O O X X O O O O O O X X O O O O O O O O O O O O O O O O O O O O O
Game of Life is een spel dat in 1970 werd uitgevonden door de Britse wiskundige John Conway. Het werd gepubliceerd in Scientific American onder de rubriek Mathematical Games van Martin Gardner. Deze spelvorm is een voorbeeld van een cellulaire automaat en wijkt af van andere spelletjes zoals monopoly, risk of schaken, in die zin dat er geen spelers zijn en dat men niet echt kan winnen of verliezen.
Het spelbord bestaat uit een rechthoekig rooster, en kan dus in een computerprogramma worden voorgesteld door een lijst van lijsten. Nadat een aantal cellen van het rooster is ingekleurd, begint het spel. Game of Life doorloopt verschillende 'generaties'. Om te bepalen of een cel in de volgende generatie gekleurd is of juist niet, wordt er een aantal regels toegepast aan de hand van de status (levend of dood) die de buurcellen hebben. Hierbij heeft elke cel in het rooster maximaal 8 buurcellen, behalve de cellen op de rand van het rooster die minder dan 8 buren hebben. Conway heeft veel geëxperimenteerd met verschillende reeksen regels om een goede balans te vinden. Met de verkeerde regels zouden namelijk meer velden (in Game of Life 'cellen' genoemd) gekleurd ('geboren') dan wit ('dood') worden, waardoor het hele hokjesveld ('rooster') gekleurd wordt. Of andersom: er gaan zoveel velden dood dat het hele gebied wit wordt. De meest gebruikte regels zijn de volgende:
- Als een levende cel door 2 of 3 levende
buurcellen omgeven wordt, blijft deze cel ook in de volgende generatie
levend, zoals de middelste cel in de onderstaande afbeelding. In dit
voorbeeld blijft de middelste cel gekleurd, want de cel wordt omgeven
door 2 andere gekleurde cellen.
- Als een levende cel door 4 of meer
levende buurcellen omgeven wordt, dan gaat deze cel dood door
overbevolking (dat wil zeggen, de cel wordt wit). Als een levende cel
door minder dan twee levende buurcellen omgeven wordt, gaat deze cel ook
dood, maar dan door eenzaamheid. Dit wordt geïllustreerd in de
onderstaande afbeelding. In dit voorbeeld gaat de middelste cel dood,
want de cel wordt door meer dan 3 of minder dan 2 gekleurde cellen
omgeven.
- Als een dode cel wordt omgeven door
precies 3 levende buurcellen, dan wordt deze dode cel in de volgende
generatie levend ('geboren'), zoals aangegeven in de afbeelding
hieronder. In dit voorbeeld wordt de middelste cel gekleurd, want de cel
wordt door exact 3 gekleurde cellen omgeven.
Al deze transformaties geschieden gelijktijdig voor alle cellen. De kunst van het spel is patronen te bedenken die bijzonder gedrag vertonen. Er zijn stabiele patronen (eenvoudigste voorbeeld: een blokje van vier). Er zijn patronen die heen en weer gaan tussen twee of meer standen. Er zijn patronen die op den duur verdwijnen of veranderen in een stabiel patroon. Interessant zijn de patronen die zich verplaatsen, zoals de glider en de glider gun.
Opgave
- Schrijf een functie toonGeneratie die de toestand van een gegeven generatie afdrukt. Deze functie heeft één verplicht argument: een lijst van lijsten die een rechthoekig rooster voorstelt. De geneste lijsten hebben allemaal dezelfde lengte en bevatten enkel Booleaanse waarden. Een generatie wordt dus voorgesteld door een lijst van rijen, waarbij elke rij zelf ook door een lijst wordt voorgesteld. Op positie $n$ staat er True als de cel op kolom $n$ in die rij leeft. Anders staat er False. De levende cellen worden bij het afdrukken voorgesteld door de letter X en de dode cellen worden voorgesteld door de letter O (niet het cijfer nul!!).
- Schrijf een functie aantalBuren die voor een gegeven generatie en een gegeven cel teruggeeft hoeveel levende buren die cel heeft. Deze functie heeft drie verplichte argumenten: het eerste argument is de gegeven generatie, het tweede argument de rij en het derde argument de kolom van de cel waarvan de buren worden opgevraagd.
- Gebruik de functie aantalBuren om een functie volgendeGeneratie te schrijven, dat de volgende generatie teruggeeft voor een gegeven generatie. Deze nieuwe generatie wordt op dezelfde manier voorgesteld als de gegeven generatie, namelijk als een lijst van lijsten. De gegeven generatie wordt als argument aan de functie doorgegeven, en wordt door de functie ook niet gewijzigd.
Onderstaand voorbeeld illustreert hoe deze functie moeten kunnen gebruikt worden.
Voorbeeld
>>> generatie = [[True] + [False] * 7 for _ in range(6)] >>> toonGeneratie(generatie) X O O O O O O O X O O O O O O O X O O O O O O O X O O O O O O O X O O O O O O O X O O O O O O O >>> aantalBuren(generatie, 0, 0) 1 >>> aantalBuren(generatie, 1, 1) 3 >>> aantalBuren(generatie, 2, 2) 0 >>> volgende = volgendeGeneratie(generatie) >>> toonGeneratie(volgende) O O O O O O O O X X O O O O O O X X O O O O O O X X O O O O O O X X O O O O O O O O O O O O O O >>> volgende = volgendeGeneratie(volgende) >>> toonGeneratie(volgende) O O O O O O O O X X O O O O O O O O X O O O O O O O X O O O O O X X O O O O O O O O O O O O O O >>> volgende = volgendeGeneratie(volgende) >>> toonGeneratie(volgende) O O O O O O O O O X O O O O O O O O X O O O O O O O X O O O O O O X O O O O O O O O O O O O O O >>> volgende = volgendeGeneratie(volgende) >>> toonGeneratie(volgende) O O O O O O O O O O O O O O O O O X X O O O O O O X X O O O O O O O O O O O O O O O O O O O O O
| Added by: | Peter Dawyndt |
| Date: | 2011-12-13 |
| Time limit: | 5s-10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


 RSS
RSS