| Submit | All submissions | Best solutions | Back to list |
PROG0355 - Well done |
Using a 7-liter and a 3-liter jug, how can you obtain exactly 5 liters of water from a well? That's a water-fetching puzzle, a familiar task in puzzle books. Most such problems can be solved fairly easy using intuition or trial-and-error. In his book Scripta Mathematica from 1948 H.D. Grossman however describes an ingenious way to generate a solution.
Let $a$ and $b$ be the sizes of the jugs (in liter), and $c$ be the number of liters that we're seeking. In the example given above $a=7$, $b=3$ and $c=5$. The positive integers $a$ and $b$ must not be same, must be relatively prime (their greatest common divisor should be equal to 1) and the volume of at least one of the jugs needs to be larger than $c$ liter. Otherwise the problem is unsolvable, trivial, or can be reduced to smaller integers.
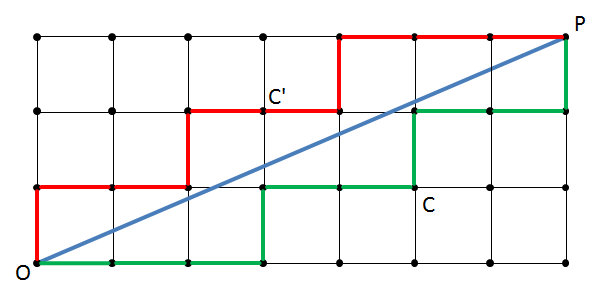
Consider a field of lattice points (points having integer coordinates) containing the line $OP$ (blue line) that connects $O$ at the point $(0, 0)$ with $P$ at the point $(a, b)$ (the point $(7, 3)$ in our example). Then draw a zigzag line $Z$ (green line) that starts at $O$ and always connects the current point with its top neighbour if this point is not above the line $OP$, or otherwise connects the current point with its right neighbour. It may be proved that $Z$ crosses the line $OP$ for the first time in $P$.
The zigzag line $Z$ now gives a map showing how to fill the jugs from the well, pour water from one jug in the other, and empty jugs, until a point is reached where one of the jugs exactly contains the number of liters we want to retrieve. Starting from $O$ and following the zigzag line, we perform the following two actions at each vertical step
- Fill the $a$-liter jug with water from the $b$-liter jug.
- Empty the $a$-liter jug. (no need to do this if the $b$-liter jug already contains $c$ liters of water)
and we perform the following two actions at each horizontal step
- Pour the content of the $b$-liter jug in the $a$-liter jug. (if the $b$-liter jug contains water)
- Fill the $b$-liter jug from the well. (no need to do this if the $a$-liter jug already contains $c$ liters of water)
We follow $Z$ until one of both jugs exactly contains the requested water volume. It may be proven that the zigzag line always contains a point $C$ where this condition is fulfilled. In our example, the map instructs us to
- Fill the 3-liter jug from the well.
- Pour the content of the 3-liter jug in the 7-liter jug.
- Fill the 3-liter jug from the well.
- Pour the content of the 3-liter jug in the 7-liter jug.
- Fill the 3-liter jug from the well.
- Fill the 7-liter jug with water from the 3-liter jug. (one more liter of water can be poured, so that the 3-liter jug still contains 2 liters of water)
- Empty the 7-liter jug.
- Pour the content of the 3-liter jug in the 7-liter jug. (the 7-liter jug now contains 2 liters of water)
- Fill the 3-liter jug from the well.
- Pour the content of the 3-liter jug in the 7-liter jug.
- The 7-liter jug now contains 5 liter.
An alternate solution can be found by drawing a second zigzag line $Z'$ (red line) on top of $OP$. This line always visits the right neightbour if that point is above the line $OP$, otherwise it visits the top neighbour. In reading this solution, we swap the roles of $a$ and $b$ given above. In our example, the alternative map instructs us to
- Fill the 7-liter jug from the well.
- Fill the 3-liter jug with water from the 7-liter jug.
- Empty the 3-liter jug.
- Fill the 3-liter jug with water from the 7-liter jug. (remains 1 liter of water in the 7-liter jug)
- Empty the 3-liter jug.
- Pour the content of the 7-liter jug in the 3-liter jug. (the 3-liter jug now contains 1 liter of water)
- Fill the 7-liter jug from the well.
- Fill the 3-liter jug with water from the 7-liter jug. (2 liters of water are poured)
- The 7-liter jug now contains 5 liter.
In his book Grossman stated that "There are always exactly two solutions which are in a sense complementary to each other."
Assignment
- Write a function position
that takes two points $p_1$ and $p_2$. Each point is represented as a
tuple containing two integers $(x, y)$. The function must return an
integer that indicates whether point $p_2$ is on (value 0), above (value
1) or below (value -1) the line that goes through the origin $(0, 0)$
and the point $p_1$.
Hint: If $p_1$ is the point $(a, b)$, the line connecting this point with the origin is described by the equation $ay - bx = 0$. For points $(x, y)$ that are above this line, the expression $ay - bx$ is positive, and for points that are below the line the expression is negative. - Write a function wellDone that takes three integers $a$, $b$ and $c$. The function must print the actions needed to retrieve exactly $c$ liters of water using an $a$-liter jug and a $b$-liter jug. Finally, the function should also print which jug has the requested volume of water. You may assume that the positive integers $a$ and $b$ are not the same, are relatively prime and that the volume of at least one of the jugs is larger than $c$ liters. Make sure that your implementation of the function prints the description of the actions in exactly the same way as in the examples below. The function must also have an optional fourth parameter alternative that indicates whether the first solution (value False, the default value) or the alternative solution (value True) should be printed.
Example
>>> position((3, 7), (3, 0)) -1 >>> position((3, 7), (0, 3)) 1 >>> position((3, 7), (6, 14)) 0 >>> wellDone(7, 3, 5) Fill the 3-liter jug from the well. Pour the content of the 3-liter jug in the 7-liter jug. Fill the 3-liter jug from the well. Pour the content of the 3-liter jug in the 7-liter jug. Fill the 3-liter jug from the well. Fill the 7-liter jug with water from the 3-liter jug. Empty the 7-liter jug. Pour the content of the 3-liter jug in the 7-liter jug. Fill the 3-liter jug from the well. Pour the content of the 3-liter jug in the 7-liter jug. The 7-liter jug now contains 5 liter. >>> wellDone(7, 3, 5, alternative=True) Fill the 7-liter jug from the well. Fill the 3-liter jug with water from the 7-liter jug. Empty the 3-liter jug. Fill the 3-liter jug with water from the 7-liter jug. Empty the 3-liter jug. Pour the content of the 7-liter jug in the 3-liter jug. Fill the 7-liter jug from the well. Fill the 3-liter jug with water from the 7-liter jug. The 7-liter jug now contains 5 liter.
References
Hoe kan je exact 5 liter water afmeten uit een bron als je enkel beschikt over een kruik van 7 liter en een kruik van 3 liter? Dit soort vragen kom je vaak tegen in puzzelboeken. Meestal kunnen dergelijke problemen vrij eenvoudig opgelost worden op basis van intuïtie of via de methode van gissen-en-missen. In het boek Scripta Mathematica uit 1948 beschrijf H.D. Grossman echter een vernuftige methode om systematisch een oplossing te genereren.
Veronderstel dat beide kruiken een volume van $a$ en $b$ liter hebben en dat we $c$ liter willen afmeten. Voor het gegeven voorbeeld is $a=7$, $b=3$ en $c=5$. Er moet gelden dat $a$ en $b$ twee verschillende positieve gehele getallen zijn, dat $a$ en $b$ relatieve priemgetallen zijn (hun grootste gemene deler is gelijk aan 1) en dat één van beide kruiken groter is dan het gevraagde volume $c$. Anders is het probleem onoplosbaar, triviaal, of kan het gereduceerd worden tot kleinere getallen.
Beschouw een veld van roosterpunten (punten met gehele coördinaten) met daarin de lijn $OP$ (blauwe lijn) die $O$ in het punt $(0, 0)$ verbindt met $P$ in het punt $(a, b)$ (het punt $(7, 3)$ in ons voorbeeld). Teken nu een zigzaglijn $Z$ (groene lijn) die vanuit $O$ vertrekt, en steeds het huidige punt verbindt met zijn bovenbuur als deze niet boven de lijn $OP$ ligt, of anders het huidige punt verbindt met zijn rechterbuur. Er kan aangetoond worden dat $Z$ voor het eerst de lijn $OP$ snijdt in het punt $P$.
De zigzaglijn $Z$ vormt nu als het ware een beschrijving om de kruiken te vullen uit de bron, in elkaar over te gieten en leeg te maken, totdat op een bepaald punt één van beide kruiken exact de gevraagde hoeveelheid water bevat. Als we starten in $O$ en de zigzaglijn volgen, dan voeren we bij elke stap omhoog de volgende twee acties uit
- Vul de $a$-liter kruik op met water uit de $b$-liter kruik.
- Giet de $a$-liter kruik leeg. (niet nodig indien de $b$-liter kruik reeds $c$ liter water bevat)
en voeren we bij elke stap naar rechts de volgende twee acties uit
- Giet de inhoud van de $b$-liter kruik in de $a$-liter kruik. (indien er water in de $b$-liter kruik zit)
- Vul de $b$-liter kruik aan de bron. (niet nodig indien de $a$-liter kruik reeds $c$ liter water bevat)
We blijven $Z$ volgen totdat één van beide kruiken exact de gevraagde hoeveelheid water bevat. Er kan aangetoond worden dat er altijd zo een punt $C$ op de zigzaglijn te vinden is. Voor ons voorbeeld moeten dus de volgende acties uitgevoerd worden
- Vul de 3-liter kruik aan de bron.
- Giet de inhoud van de 3-liter kruik in de 7-liter kruik.
- Vul de 3-liter kruik aan de bron.
- Giet de inhoud van de 3-liter kruik in de 7-liter kruik.
- Vul de 3-liter kruik aan de bron.
- Vul de 7-liter kruik op met water uit de 3-liter kruik. (er kan nog 1 liter water overgegoten worden, zodat de 3-liter kruik nog 2 liter water bevat)
- Giet de 7-liter kruik leeg.
- Giet de inhoud van de 3-liter kruik in de 7-liter kruik. (de 7-liter kruik bevat nu 2 liter water)
- Vul de 3-liter kruik aan de bron.
- Giet de inhoud van de 3-liter kruik in de 7-liter kruik.
- De 7-liter kruik bevat nu 5 liter.
Er kan een alternatieve oplossing gevonden worden door een tweede zigzaglijn $Z'$ (rode lijn) te tekenen boven de lijn $OP$. Deze lijn gaat steeds naar de rechterbuur indien dat punt boven de lijn $OP$ ligt, anders naar de bovenbuur. De oplossing die we op deze manier aflezen kan gevonden worden door de rol van $a$ en $b$ om te wisselen in bovenstaande omschrijvingen. De alternatieve oplossing voor ons voorbeeld wordt dan
- Vul de 7-liter kruik aan de bron.
- Vul de 3-liter kruik op met water uit de 7-liter kruik.
- Giet de 3-liter kruik leeg.
- Vul de 3-liter kruik op met water uit de 7-liter kruik. (er zit nu nog 1 liter water in de 7-liter kruik)
- Giet de 3-liter kruik leeg.
- Giet de inhoud van de 7-liter kruik in de 3-liter kruik. (de 3-liter kruik bevat nu 1 liter water)
- Vul de 7-liter kruik aan de bron.
- Vul de 3-liter kruik op met water uit de 7-liter kruik. (er wordt dus 2 liter water overgegoten)
- De 7-liter kruik bevat nu 5 liter.
Grossman zei hierover in zijn boek "There are always exactly two solutions which are in a sense complementary to each other."
Opgave
- Schrijf een functie positie
waaraan twee punten $p_1$ en $p_2$ moeten doorgegeven worden. Elk punt
wordt voorgesteld door een tuple van twee natuurlijke getallen $(x, y)$.
De functie moet een geheel getal teruggeven dat aangeeft of het punt
$p_2$ op (waarde 0), boven (waarde 1) of onder (waarde -1) de rechte
ligt die door de oorsprong $(0, 0)$ en het punt $p_1$ gaat.
Hint: Als $p_1$ het punt $(a, b)$ is, dan wordt de rechte die dit punt verbindt met de oorsprong beschreven door de vergelijking $ay - bx = 0$. Voor punten boven deze rechte is $ay - bx$ positief, en voor punten eronder is deze waarde negatief. - Schrijf een functie broncode waaraan de natuurlijke getallen $a$, $b$ en $c$ moeten doorgegeven worden. De functie moet de acties uitschrijven die nodig zijn om exact $c$ liter water af te meten als je beschikt over een $a$-liter kruik en een $b$-liter kruik. Finaal moet ook uitgeschreven worden welke kruik de gevraagde hoeveelheid water bevat. Je mag er hierbij van uitgaan dat $a$ en $b$ verschillende positieve gehele getallen zijn, dat $a$ en $b$ relatieve priemgetallen zijn en dat één van beide kruiken groter is dan het gevraagde volume $c$. Zorg ervoor dat je implementatie dezelfde omschrijvingen van de acties gebruikt als in onderstaande voorbeeld staat aangegeven. De functie moet ook een optionele vierde parameter alternatief hebben, die aangeeft of de eerste oplossing (waarde False, de standaardwaarde) dan wel de alternatieve oplossing (waarde True) moet uitgeschreven worden.
Voorbeeld
>>> positie((3, 7), (3, 0)) -1 >>> positie((3, 7), (0, 3)) 1 >>> positie((3, 7), (6, 14)) 0 >>> broncode(7, 3, 5) Vul de 3-liter kruik aan de bron. Giet de inhoud van de 3-liter kruik in de 7-liter kruik. Vul de 3-liter kruik aan de bron. Giet de inhoud van de 3-liter kruik in de 7-liter kruik. Vul de 3-liter kruik aan de bron. Vul de 7-liter kruik op met water uit de 3-liter kruik. Giet de 7-liter kruik leeg. Giet de inhoud van de 3-liter kruik in de 7-liter kruik. Vul de 3-liter kruik aan de bron. Giet de inhoud van de 3-liter kruik in de 7-liter kruik. De 7-liter kruik bevat nu 5 liter. >>> broncode(7, 3, 5, alternatief=True) Vul de 7-liter kruik aan de bron. Vul de 3-liter kruik op met water uit de 7-liter kruik. Giet de 3-liter kruik leeg. Vul de 3-liter kruik op met water uit de 7-liter kruik. Giet de 3-liter kruik leeg. Giet de inhoud van de 7-liter kruik in de 3-liter kruik. Vul de 7-liter kruik aan de bron. Vul de 3-liter kruik op met water uit de 7-liter kruik. De 7-liter kruik bevat nu 5 liter.
Bronnen
| Added by: | Peter Dawyndt |
| Date: | 2013-03-30 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


 RSS
RSS