| Submit | All submissions | Best solutions | Back to list |
PROG0424 - Pythagorean triples |
A Pythagorean triple $(a, b, c)$ consists of three strictly positive integers $a$, $b$ and $c$, for which $a^2 + b^2 = c^2$. The name is derived from the Pythagorean theorem, as Pythagorean triples describe the three integer side lengths of a right triangle, where $c$ is the length of the hypothenuse.
A well-known example is $(3, 4, 5)$, but also its multiples such as $(6, 8, 10)$ and $(9, 12, 15)$ are Pythagorean triples. In general, if $(a, b, c)$ is a Pythagorean triple, so is $(ka, kb, kc)$ for any positive integer $k$. A primitive Pythagorean triple $(a, b, c)$ is one in which $a$, $b$ and $c$ are coprime. As an example, there are four Pythagorean triples $(a, b, c)$ for which $a + b + c = 240$: $(15, 112, 113)$, $(40, 96, 104)$, $(48, 90, 102)$ and $(60, 80, 100)$.
Babylonian clay tablets dating from the time of Hammurabi already mention Pythagorean triples. The tablet Plimpton 322, for example, lists 15 triplets, including $(56, 90, 106)$, $(119, 120, 169)$ and even $(12709, 13500, 18541)$. Pythagorean triples were also known in India. The earliest Baudhayana-Sulbasutra (dating back to the sixth century before Christ) contains five such triples.
Input
A number $n \in \mathbb{N}$.
Output
A list of all Pythagorean triples $(a, b, c)$ for which $a \leq b$ and $a + b + c = n$. These triples must be written as (a, b, c), each on a separate line and sorted in increasing order according to $a$, then $b$ and then $c$.
Example
Input:
240
Output:
(15, 112, 113) (40, 96, 104) (48, 90, 102) (60, 80, 100)
Een Pythagorees drietal $(a, b, c)$ bestaat uit drie strikt positieve natuurlijke getallen $a$, $b$ en $c$ waarvoor geldt dat $a^2 + b^2 = c^2$. De naam werd afgeleid van de stelling van Pythagoras, aangezien dergelijke drietallen kunnen optreden als lengtes van de zijden van een rechthoekige driehoek met $c$ als lengte van de schuine zijde.
Naast het drietal $(3, 4, 5)$ vormen ook veelvouden hiervan, zoals $(6, 8, 10)$ en $(9, 12, 15)$ Pythagorese drietallen. Algemeen is met $(a, b, c)$ ook $(ka, kb, kc)$ voor elk positief natuurlijk getal $k$ een Pythagorees drietal. Een Pythagorees drietal $(a, b, c)$ wordt primitief genoemd als $a$, $b$ en $c$ geen deler anders dan 1 gemeen hebben. Er bestaan bijvoorbeeld vier Pythagorese drietallen $(a, b, c)$ waarvoor de $a + b + c = 240$: $(15, 112, 113)$, $(40, 96, 104)$, $(48, 90, 102)$ en $(60, 80, 100)$.
Op kleitabletten uit de tijd van Hammurabi komen al Pythagorese drietallen voor. Op het tablet Plimpton 322 staan bijvoorbeeld 15 drietallen, waaronder $(56, 90, 106)$, $(119, 120, 169)$ en zelfs $(12709, 13500, 18541)$. Ook in India kende men zulke getallen. In de Baudhayana-Sulbasutra uit de 6e eeuw voor Christus staan vijf zulke drietallen.
Invoer
Een getal $n \in \mathbb{N}$.
Uitvoer
Een lijst van alle Pythagorese drietallen $(a, b, c)$ waarvoor $a \leq b$ en $a + b + c = n$. De drietallen moeten uitgeschreven worden onder de vorm (a, b, c), elk op een afzonderlijk regel en oplopend gesorteerd volgens $a$, dan $b$ en dan $c$.
Voorbeeld
Invoer:
240
Uitvoer:
(15, 112, 113) (40, 96, 104) (48, 90, 102) (60, 80, 100)
| Added by: | Peter Dawyndt |
| Date: | 2013-09-11 |
| Time limit: | 30s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

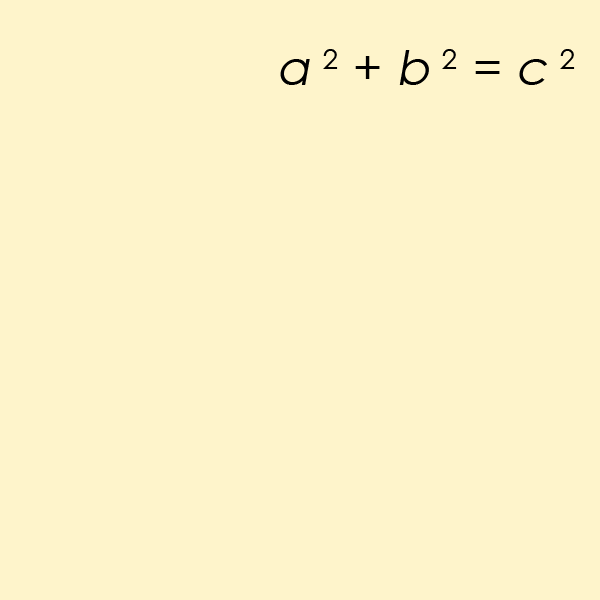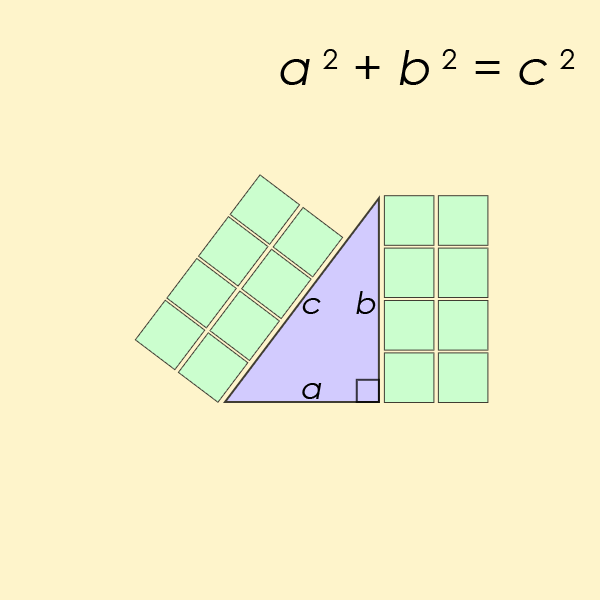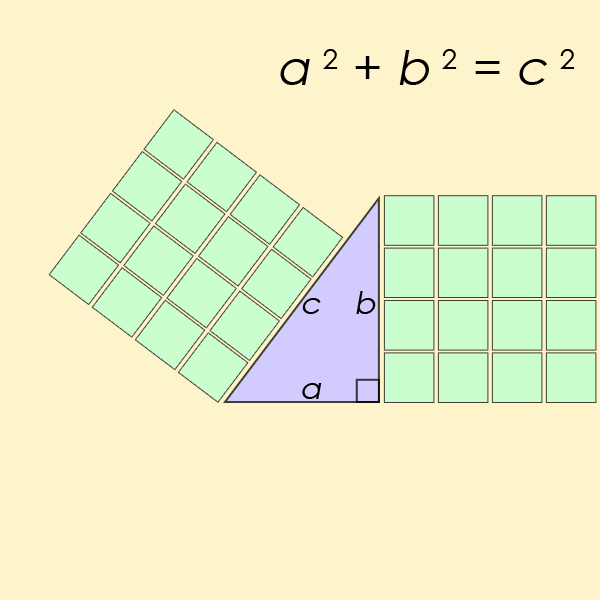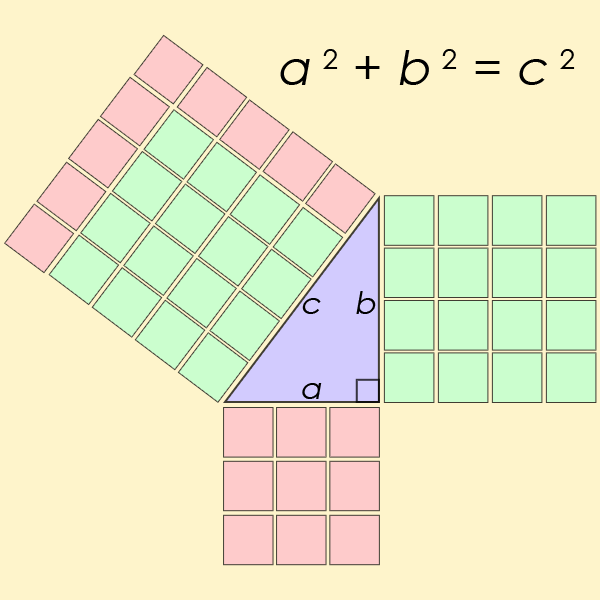
 RSS
RSS