| Submit | All submissions | Best solutions | Back to list |
PROG0451 - Ice core |
An ice core is a cylinder shaped sample that comes from an ice cap, usually from the polar regions or from a glacier. Seeing that ice caps are formed by an accumulation of yearly snow layers, they are built out of ice from different years where the under layers are older than the upper layers. Thanks to analysis of the properties of the ice and the gas composition of crystallized air bulbs that are enclosed in the ice, a climatological reconstruction can be made of the period in which the ice core was formed. Based on the concentrations and the isotopes of carbon monoxide and methane, for example, one can map out the evolution of the local temperature and the atmospheric composure.
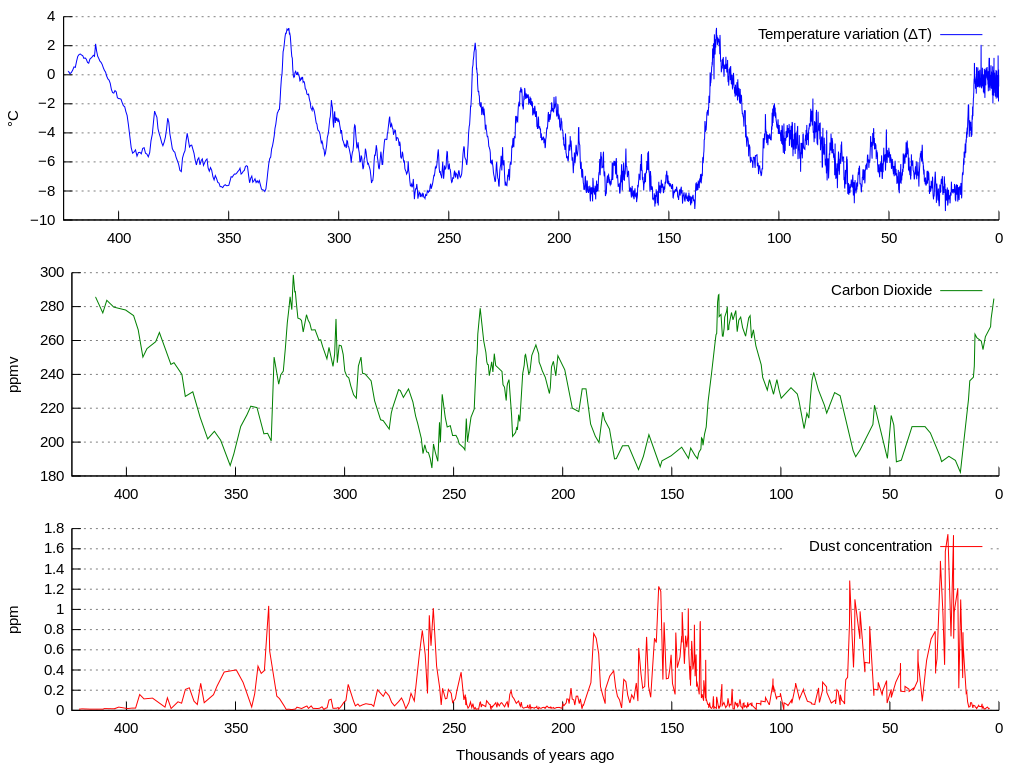
The picture above shows the evolution of temperature (blue), the concentration of carbon monoxide (green) and the amount of particles that were fixed (red) in the Vostok ice cap (Antarctica) ofer a period of the past 420.000 years. Here, a number of climatological cycles can be seen with the naked eye. However, the course of such time-series contains too much noise to immediately analyze them with a computer. This noise can be suppressed by simple mathematical techniques to level off the curves.
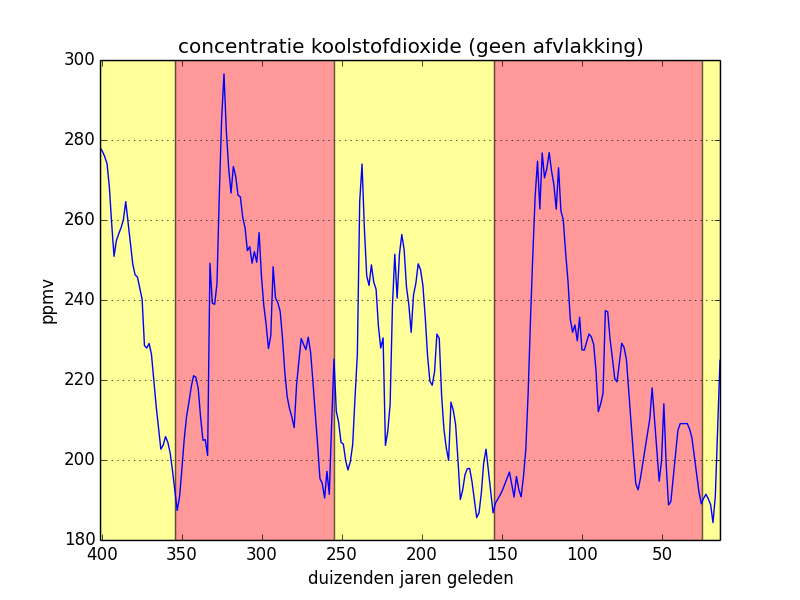
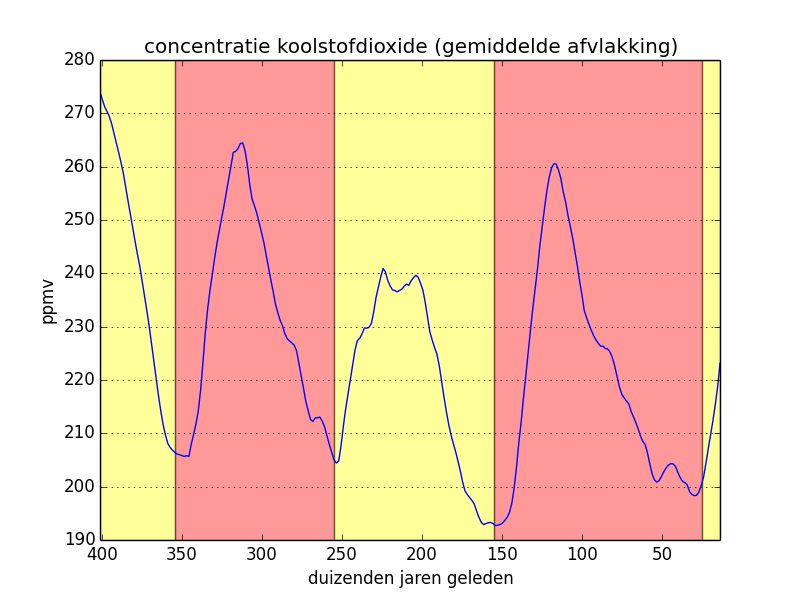
In the left-hand figure below we have copied the original values of the carbon monoxide concentration and we have indicated the climatological cycles. In the middle figure, we have applied a mean flattening to the original values and the right-hand figure is a result of a triangle flattening. In the last two cases, the periodical character of the curve is pronounced even more clearly.
Assignment
We have determined the concentration of a certain property (e.g. the concentration of carbon monoxide) alongside consecutive points of an ice core. The values on these measurement points were bundled in a list or tuple. Your assignment is to level off these measuring values so that it is can be analyzed more easily by a computer. Work as follows:
- Say we have a sequence of $m \in \mathbb{N}_0$ consecutive measurements $x_i \in \mathbb{R}$ ($1 \leq i \leq m$). The weighted average $s$ of these measurements is obtained by linking $w_i \in \mathbb{R}$ ($1 \leq i \leq m$) to every measurement, and calculating the following $$s = \frac{\displaystyle\sum_{i=1}^m w_i x_i}{\displaystyle\sum_{i=1}^m w_i}$$ For the sequence of measurements $(4, 3, 7)$ and the sequence of weights $(1, 2, 1)$ the weighted average is $$ s = \frac{4 \times 1 + 3 \times 2 + 7 \times 1}{1 + 2 + 1} = 4.25 $$ Write a function weightedAverage to which two lists or tuples must be given. These arguments respectively represent a sequence of measurements $x_i$ ($1 \leq i \leq m$) and a sequence of weights $w_i$ ($1 \leq i \leq m$). If the length of the given sequences is unequal, the function must raise an AssertionError with the message sequences should have equal length. Otherwise, the function should print the weighted average $s$ of the given measurements, based on the weights given.
- Write a function smooth
to which two lists or tuples must be given. The first argument
represents a sequence of $n \in \mathbb{N}_0$ consecutive measurements
$x_i \in \mathbb{R}$ ($1 \leq i \leq n$), and the second argument
represents a sequence of $m \in \mathbb{N}_0$ weights $w_i \in
\mathbb{R}$ ($1 \leq i \leq m$). As a result, the function should print
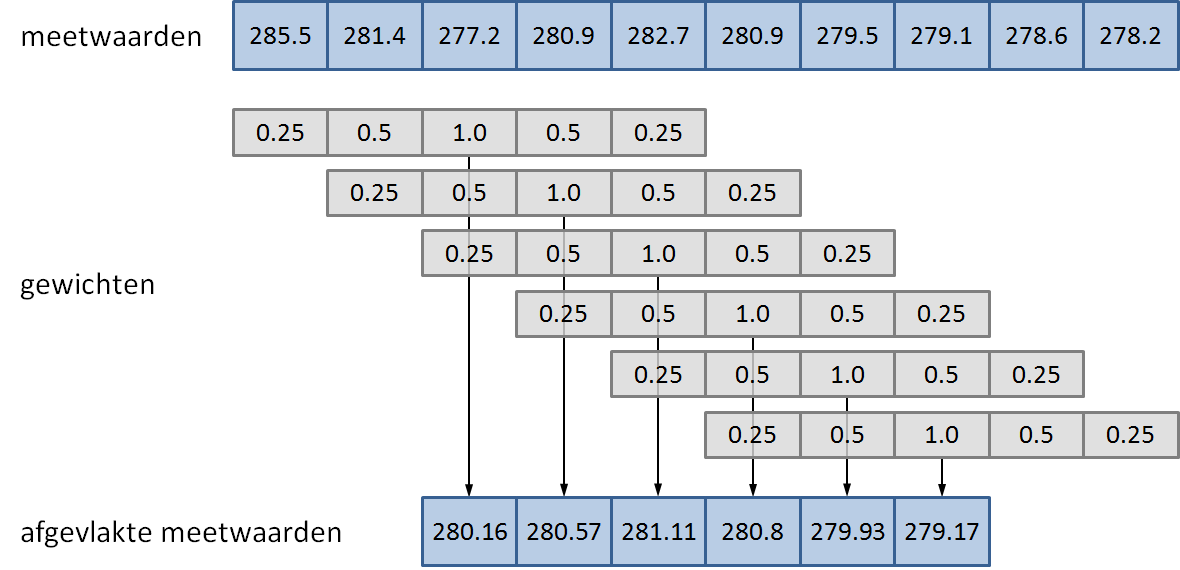
a new list, that contains the weighted averages of all $m$ consecutive
measurements with the given weights (see figure below). If $n < m$,
an empty list must be printed.
- If all weights used for flattening have the same value $w$ ($w \neq 0$), the weighted average is nothing but a normal mean of a measurement and a number of neighbouring measured values left and right of the measurement. If we use the list of weights [1, 1, 1, 1, 1], for example, 5 measurements (the measuring point and two points left and right) are averaged. This is called the mean flattening with window width $v = 5$. Analogously, the list with weights [1, 1, 1, 1, 1, 1, 1] is used for the mean flattening with window width $v = 7$. Use the function smooth to write a function smoothAverage to which an obligatory list or tuple of measurements and an optional window width $v$ (argument window; default value 5) must be given. The function must print a flattened list of measurements that is the result of applying the mean flattening with window width $v$.
- For leveling off triangles a sequence of weights is used that increases from 1 in the first part, and halfway it starts decreasing again. For example, the triangle flattening with window width $v=5$ uses the weights [1, 2, 3, 2, 1], the triangle flattening with window width $v=7$ uses the weights [1, 2, 3, 4, 3, 2, 1], and so on. Use the function smooth to write a function smoothTriangle to which an obligatory list or tuple of measurements and an optional window width $v$ (argument window; default value 5) must be given. If the given window width is even, the function should raise an AssertionError with the message window size must be odd value. Otherwise the function must print the flattened list of measurements that is the result after applying the triangle flattening with window width $v$.
Example
In the interactive session below we have rounded off the floating point numbers in order to retain a brief example. In the assignment we do not ask to round off numbers.
>>> CO2 = [285.5, 281.4, 277.2, 280.9, 282.7] >>> weights = [0.5, 1.0, 0.5] >>> weightedAverage(CO2, weights ) Traceback (most recent call last): AssertionError: sequences should have equal length >>> weights = [0.25, 0.5, 1.0, 0.5, 0.25] >>> weightedAverage(CO2, weights ) 280.16 >>> weightedAverage((4.0, 3.0, 7.0), (1.0, 2.0, 1.0)) 4.25 >>> CO2 = [285.5, 281.4, 277.2, 280.9, 282.7, 280.9, 279.5, 279.1, 278.6, 278.2] >>> smooth(CO2, weights) [280.16, 280.57, 281.11, 280.8, 279.93, 279.17] >>> smoothAverage(CO2) [281.54, 280.62, 280.24, 280.62, 280.16, 279.26] >>> smoothAverage(CO2, window=4) [281.25, 280.55, 280.425, 281.0, 280.55, 279.525, 278.85] >>> smoothTriangle(CO2) [280.489, 280.533, 280.933, 280.789, 279.978, 279.178] >>> smoothTriangle(CO2, window=4) Traceback (most recent call last): AssertionError: window size must be odd value >>> smoothTriangle(CO2, window=3) [281.375, 279.175, 280.425, 281.8, 281.0, 279.75, 279.075, 278.625]
Sources
- Petit JR, Jouzel J, Raynaud D, Barkov NI, Barnola JM, Basile
I, Bender M, Chappellaz J, Davis M, Delaygue G, Delmotte M, Kotlyakov
VM, Legrand M, Lipenkov VY, Lorius C, Pépin L, Ritz C, Saltzman
E, Stievenard M (1999). Climate and atmospheric history of
the past 420,000 years from the Vostok ice core, Antarctica. Nature
399, 429-436.

- Jouzel J, Petit JR, Souchez R, Barkov NI, Lipenkov VY,
Raynaud D, Stievenard M, Vassiliev NI, Verbeke V, Vimeux F (1999).
More than 200 meters of lake ice above subglacial Lake Vostok,
Antarctica. Science 286(5447),
2138-2141.

Een ijskern is een cilindervormig monster afkomstig van een ijskap, meestal uit de poolgebieden of van een gletsjer. Aangezien ijskappen zich vormen door de opeenstapeling van jaarlijkse sneeuwlagen, zijn ze opgebouwd uit ijs van verschillende jaren waarbij de onderste lagen ouder zijn dan de bovenste. Door analyse van de eigenschappen van het ijs en de gassamenstelling van gekristalliseerde luchtbelletjes die in het ijs ingesloten zitten, kan een klimatologische reconstructie gemaakt worden van de periode waarin de ijskern gevormd werd. Op basis van de concentraties en de isotopen van koolstofmonoxide en methaan kan men bijvoorbeeld de evolutie van de lokale temperatuur en de atmosferische samenstelling in kaart brengen.
Bovenstaande figuur toont de evolutie van de temperatuur (blauw), de concentratie koolstofdioxide (groen) en de hoeveelheid stofdeeltjes die zich in het ijs hebben vastgezet (rood) in de ijskap van Vostok (Antarctica) over een periode van de laatste 420.000 jaar. Hierin kunnen met het blote oog reeds een aantal klimatologische cycli herkend worden. Het verloop van dergelijke tijdsreeksen bevat echter te veel ruis om ze rechtstreeks door een computer te laten analyseren. Deze ruis kan onderdrukt worden door toepassing van eenvoudige wiskundige technieken om de curves af te vlakken.
In de linker figuur hieronder hebben de we originele meetwaarden van de concentratie koolstofmonoxide overgenomen, en daarbij hebben we ook de opeenvolgende klimatologische cycli aangeduid. In de middelste figuur hebben we een gemiddelde afvlakking toegepast op de originele meetwaarden en de rechter figuur is het resultaat van een driehoeksafvlakking. In de laatste twee gevallen is het periodieke karakter van de curve nog duidelijker uitgesproken.
Opgave
Langs opeenvolgende punten van een ijskern hebben we de concentratie van een bepaalde eigenschap (bv. de concentratie koolstofdioxide) bepaald. De waarden op deze meetpunten werden gebundeld in een lijst of een tuple. Gevraagd wordt om deze meetwaarden af te vlakken zodat ze makkelijker met de computer kunnen geanalyseerd worden. Hiervoor ga je als volgt te werk:
- Stel dat we beschikken over een reeks van $m \in \mathbb{N}_0$ opeenvolgende meetwaarden $x_i \in \mathbb{R}$ ($1 \leq i \leq m$). Het gewogen gemiddelde $s$ van deze meetwaarden wordt bekomen door aan elke meetwaarde een gewicht $w_i \in \mathbb{R}$ ($1 \leq i \leq m$) te koppelen, en de volgende berekening uit te voeren $$s = \frac{\displaystyle\sum_{i=1}^m w_i x_i}{\displaystyle\sum_{i=1}^m w_i}$$ Voor de reeks meetwaarden $(4, 3, 7)$ en de reeks gewichten $(1, 2, 1)$ is het gewogen gemiddelde dus gelijk aan $$ s = \frac{4 \times 1 + 3 \times 2 + 7 \times 1}{1 + 2 + 1} = 4.25 $$ Schrijf een functie gewogenGemiddelde waaraan twee lijsten of tuples moeten doorgegeven worden. Deze argumenten stellen respectievelijk een reeks meetwaarden $x_i$ ($1 \leq i \leq m$) en een reeks gewichten $w_i$ ($1 \leq i \leq m$) voor. Indien de gegeven reeksen niet even lang zijn, dan moet de functie een AssertionError opwerpen met de boodschap reeksen moeten even lang zijn. Anders moet de functie het gewogen gemiddelde $s$ van de gegeven meetwaarden teruggeven, op basis van de gegeven gewichten.
- Schrijf een functie afvlakken
waaraan twee lijsten of tuples moeten doorgegeven worden. Het eerste
argument stelt een reeks van $n \in \mathbb{N}_0$ opeenvolgende
meetwaarden $x_i \in \mathbb{R}$ ($1 \leq i \leq n$) voor, en het tweede
argument een reeks van $m \in \mathbb{N}_0$ gewichten $w_i \in
\mathbb{R}$ ($1 \leq i \leq m$). De functie moet als resultaat een
nieuwe lijst teruggeven, die de gewogen gemiddelden bevat van alle $m$
opeenvolgende meetwaarden met de gegeven gewichten (zie onderstaande
figuur). Indien geldt dat $n < m$, dan moet de lege lijst
teruggegeven worden.
- Als alle gewichten die gebruikt worden bij het afvlakken eenzelfde waarde $w$ ($w \neq 0$) hebben, dan is het gewogen gemiddelde niets anders dan een gewoon gemiddelde van een meetwaarde en een aantal naburige meetwaarden links en rechts van het meetpunt. Als we bijvoorbeeld de lijst van gewichten [1, 1, 1, 1, 1] gebruiken, dan worden 5 meetwaarden uitgemiddeld (meetpunt en twee punten links en rechts). Dit wordt gemiddelde afvlakking genoemd met vensterbreedte $v = 5$. Analoog wordt bij gemiddelde afvlakking met vensterbreedte $v = 7$ de lijst gewichten [1, 1, 1, 1, 1, 1, 1] gebruikt. Gebruik de functie afvlakken om een functie afvlakkenGemiddelde te schrijven waaraan verplicht een lijst of tuple van meetwaarden en optioneel een vensterbreedte $v$ (argument venster; standaardwaarde 5) moeten doorgegeven worden. De functie moet als resultaat de afgevlakte lijst van meetwaarden teruggeven die resulteert na toepassing van gemiddelde afvlakking met vensterbreedte $v$.
- Bij driehoeksafvlakking wordt gebruik gemaakt van een reeks gewichten die in het eerste deel oploopt vanaf 1, en halverwege terug begint af te lopen. Zo maakt driehoeksafvlakking met vensterbreedte $v=5$ gebruik van de gewichten [1, 2, 3, 2, 1], gebruikt driehoeksafvlakking met vensterbreedte $v=7$ de gewichten [1, 2, 3, 4, 3, 2, 1], enzoverder. Gebruik de functie afvlakken om een functie afvlakkenDriehoek te schrijven waaraan verplicht een lijst of tuple van meetwaarden en optioneel een vensterbreedte $v$ (argument venster; standaardwaarde 5) moeten doorgegeven worden. Indien de gegeven vensterbreedte even is, moet de functie een AssertionError opwerpen met boodschap vensterbreedte moet oneven zijn. Anders moet de functie als resultaat de afgevlakte lijst van meetwaarden teruggeven die resulteert na toepassing van driehoeksafvlakking met vensterbreedte $v$.
Voorbeeld
In onderstaande interactieve sessie hebben we de floating point getallen afgerond om de voorbeelden beknopt te houden. In de opgave wordt niet gevraagd om een dergelijke afronding uit te voeren.
>>> CO2 = [285.5, 281.4, 277.2, 280.9, 282.7] >>> gewichten = [0.5, 1.0, 0.5] >>> gewogenGemiddelde(CO2, gewichten) Traceback (most recent call last): AssertionError: reeksen moeten even lang zijn >>> gewichten = [0.25, 0.5, 1.0, 0.5, 0.25] >>> gewogenGemiddelde(CO2, gewichten) 280.16 >>> gewogenGemiddelde((4.0, 3.0, 7.0), (1.0, 2.0, 1.0)) 4.25 >>> CO2 = [285.5, 281.4, 277.2, 280.9, 282.7, 280.9, 279.5, 279.1, 278.6, 278.2] >>> afvlakken(CO2, gewichten) [280.16, 280.57, 281.11, 280.8, 279.93, 279.17] >>> afvlakkenGemiddelde(CO2) [281.54, 280.62, 280.24, 280.62, 280.16, 279.26] >>> afvlakkenGemiddelde(CO2, venster=4) [281.25, 280.55, 280.425, 281.0, 280.55, 279.525, 278.85] >>> afvlakkenDriehoek(CO2) [280.489, 280.533, 280.933, 280.789, 279.978, 279.178] >>> afvlakkenDriehoek(CO2, venster=4) Traceback (most recent call last): AssertionError: vensterbreedte moet oneven zijn >>> afvlakkenDriehoek(CO2, venster=3) [281.375, 279.175, 280.425, 281.8, 281.0, 279.75, 279.075, 278.625]
Bronnen
- Petit JR, Jouzel J, Raynaud D, Barkov NI, Barnola JM, Basile
I, Bender M, Chappellaz J, Davis M, Delaygue G, Delmotte M, Kotlyakov
VM, Legrand M, Lipenkov VY, Lorius C, Pépin L, Ritz C, Saltzman
E, Stievenard M (1999). Climate and atmospheric history of
the past 420,000 years from the Vostok ice core, Antarctica. Nature
399, 429-436.

- Jouzel J, Petit JR, Souchez R, Barkov NI, Lipenkov VY,
Raynaud D, Stievenard M, Vassiliev NI, Verbeke V, Vimeux F (1999).
More than 200 meters of lake ice above subglacial Lake Vostok,
Antarctica. Science 286(5447),
2138-2141.

| Added by: | Peter Dawyndt |
| Date: | 2014-01-21 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |



 RSS
RSS